Pendel
Die Pendelstäbe bestehen aus 6 mm Buchenholz. Die beiden oberen Stäbe sind lose durch den unteren Steg
gesteckt. Die Längenveränderung erfolgt über den 4 mm Gewindestab mit Stellmutter.Die oberen Stäbe sind 590 mm und die
unteren 330 mm lang. Der Gewindestab hat eine Länge von 110 mm.
| Pendellänge | ||||||||||||||||||||||||||||||||||||
Die Länge eines mathematischen Pendels berechnet sich wie folgt:
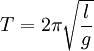 Bei T=2 Sekunden ergibt sich eine Pendellänge von 0,994 m. Diese Formel vergessen wir gleich wieder, da sie in der Praxis nicht brauchbar ist. Besser ist folgende: 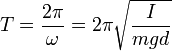 I ist das Massenträgheitsmoment m die Masse des Pendels d der Abstand des Massenmittelpunks vom Drehpunkt g ist 9,81 Hier erkennt man das die Schwingungsdauer sowohl von der Masse als auch von der Länge abhängig ist. Um die erste Formel wieder ins Spiel zu bringen kann man auch mit der reduzierten Pendellänge arbeiten.  Die Berechnung von I ist die Summe aller Massen mal dem Quadrat des Abstandes. Hier hilft die Integralrechnung weiter. Wer das nicht kann oder möchte kann sich näherungsweise so behelfen, daß er die Summe der Teilmassen x Quadrat der Entfernungen berechnet. Beispiel Rundstab 1 m lang in 10 Teilen
T=2*PI*wurzel(1/3*m/(m*9,81*0,5)) T=2*PI*wurzel(1/3/(9,81*0,5)) T=1,6379... entspricht ca. 73 Schläge |
Die Aufhängung. Innendurchmesser 50 mm. Außendurchmesser 70 mm.
